Risk is an important consideration in holding any portfolio. The risk in holding securities is generally associated with the possibility that realised returns will be less than the returns expected.

Risks can be classified as Systematic risks and Unsystematic risks.

• Unsystematic risks:
  These are risks that are unique to a firm or industry. Factors such as management capability, consumer preferences, labour, etc. contribute to unsystematic risks. Unsystematic risks are controllable by nature and can be considerably reduced by sufficiently diversifying one's portfolio.
• Systematic risks:
  These are risks associated with the economic, political, sociological and other macro-level changes. They affect the entire market as a whole and cannot be controlled or eliminated merely by diversifying one's portfolio.

What is Beta?

The degree to which different portfolios are affected by these systematic risks as compared to the effect on the market as a whole, is different and is measured by Beta. To put it differently, the systematic risks of various securities differ due to their relationships with the market. The Beta factor describes the movement in a stock's or a portfolio's returns in relation to that of the market returns. For all practical purposes, the market returns are measured by the returns on the index (Nifty, Mid-cap etc.), since the index is a good reflector of the market.

Methodology / Formula

Beta is calculated as :

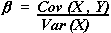
where,

Y is the returns on your portfolio or stock - DEPENDENT VARIABLE

X is the market returns or index - INDEPENDENT VARIABLE

Variance is the square of standard deviation.

Covariance is a statistic that measures how two variables co-vary, and is given by:

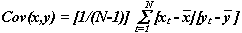
Where, N denotes the total number of observations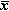, and and 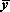respectively represent the arithmetic averages of x and y.

In order to calculate the beta of a portfolio, multiply the weightage of each stock in the portfolio with its beta value to arrive at the weighted average beta of the portfolio

Standard Deviation

Standard Deviation is a statistical tool, which measures the variability of returns from the expected value, or volatility. It is denoted by sigma(s) . It is calculated using the formula mentioned below:

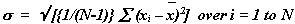
Where, 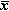is the sample mean, xi’s are the observations (returns), and N is the total number of observations or the sample size.